非线性偏微分方程(NLPDEs)模型出现在现实世界中的许多物理现象中,也运用在丰富的科学领域里,如流体动力学、非线性光纤、核物理、电磁学、医学、金融、数学生物科学等。为了通过NLPDEs的定性和定量特征来具体理解物理现象,研究这些方程的精确解是至关重要的。与常系数方程相比,变系数方程更为复杂,可以在现实生活中模拟更多的物理现象,特别是在考虑边界和介质的不均匀性时所得到的孤子在自然界中无处不在,出现在不同的系统中,如浅水波、DNA激发、玻色-爱因斯坦凝聚物中的物质波和非线性光学中的超短脉冲等。经典的伯格斯方程发生在非线性声学、气体动力学、交通流动和流体力学中。利用伯格斯方程模拟非平面激波的形成和衰减,在流体动力学研究中是非常热点的问题。人们对该方程的解析方法进行了大量的研究工作。
近日,我校商学院戚建明博士和其指导的硕士研究生朱清昊同学通过$\frac{G’}{G^2}$-展开和雅可比椭圆函数两种不同的方法,发现了变系数伯格斯方程的精确波解的多种形式,得到了前人研究工作中没有发现的很多新解,如$u_{13},u_{14},u_{511},u_{512},u_{513},u_{514}$等。最重要的是,在求解过程中运用了双周期雅可比椭圆函数思想,这是以前在寻找非线性变系数伯格斯方程时从未见过的。这些新的精确孤子解包含以三角函数、有理函数和雅可比椭圆函数、双曲函数的形式导出的变系数,显示了与原有结果许多不同类型的新结果,如湮灭、抛物型扭结、弯曲型扭结、斜形、激波孤子等。
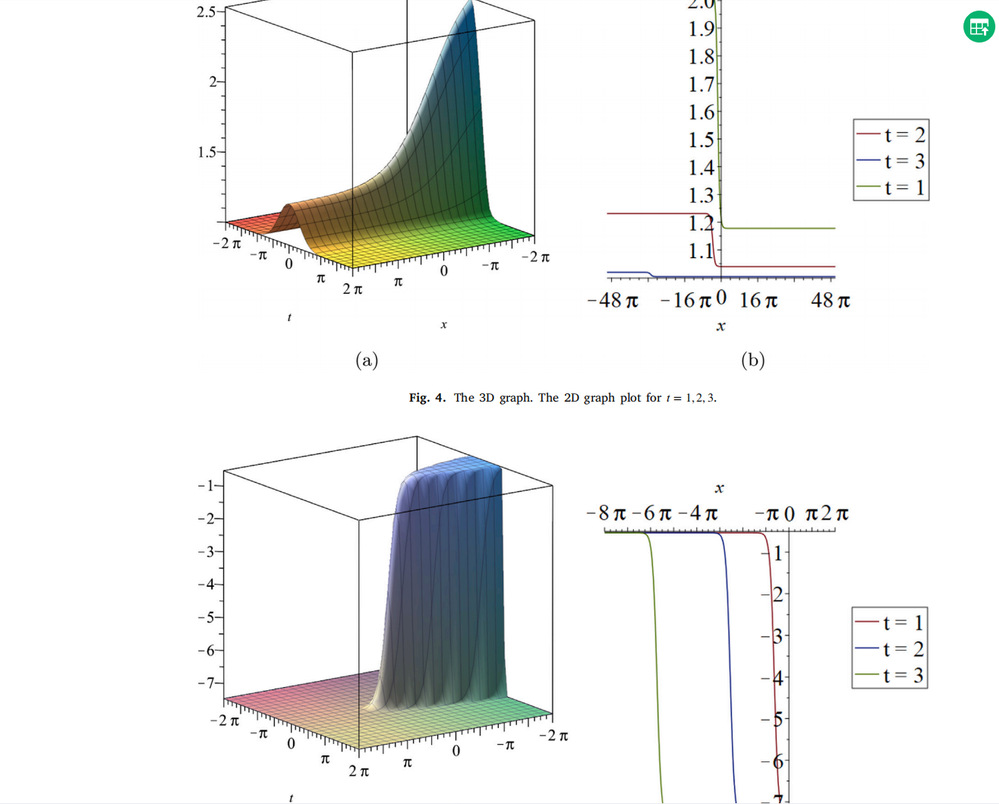
该研究运用了计算机软件制作的三维或二维图像,更加形象地刻画了孤子传输的物理动力学行为,研究中所有物理行为的分析和推断都建立于严格的数学计算结果之上。在未来,上述两种方法可用于研究其他具有变系数的非线性方程,同时该研究方法和结果也可以帮助研究人员在等离子体冲击波、非线性动力学、非线性电路传输模型等多方面研究领域寻找更多不同形式的和不同类型的传播孤子。
该研究成果以“Further results about the non-traveling wave exact solutions of nonlinear Burgers equation with variable coefficients”为题,发表在国际SCI期刊《Results in Physics》(JCR一区,中科院2022年升级版2区)上。《Results in Physics》期刊是国际著名出版商Elsevier为聚焦物理学领域相关的原创性科研成果而创办的学术期刊。上海电机学院商学院是该成果的唯一完成单位,戚建明老师为该论文的第一作者和通讯作者,朱清昊同学为第二作者。(供稿:科技处)
论文链接:https://doi.org/10.1016/j.rinp.2023.106285